解析 Temperature 与 Top P：如何掌控大模型的输出随机性

前言

在AI时代，大语言模型（LLM）如 ChatGPT 或Gemini 已成为我们的“数字大脑”。如果你经常使用这些大模型，那你肯定见过Temperature 和 TopP 这两个参数。比如 ChatGPT 的API文档就有介绍：

根据描述：

Temperature（温度）： 取值在 0 到 2 之间。较高的值（如 0.8）将使输出更加随机，而较低的值（如 0.2）将使输出更加集中和确定。

Top P（核采样）： 温度采样的替代方法。模型仅考虑概率质量排名前 P% 的标记的结果。例如，0.1 表示仅考虑概率排名前 10% 的标记。

看到这里，你可能觉得已经懂了：它们就是控制随机性的开关嘛。值越高越发散，值越低越保守。

但仔细一想，问题来了：

  1. 为什么值越高越随机，越低越稳定？背后的数学原理是什么？
  2. 如果它们控制的都是随机性，为什么需要两个参数？
  3. 如果把一个调高，另一个调低，效果会中和吗？
  4. 它们是协同工作，还是在完全不同的维度产生影响？

带着这些问题，我们将拆解这两个“黑盒子”，从大模型的底层生成原理出发，彻底搞懂它们如何掌控 AI 的每一次开口。

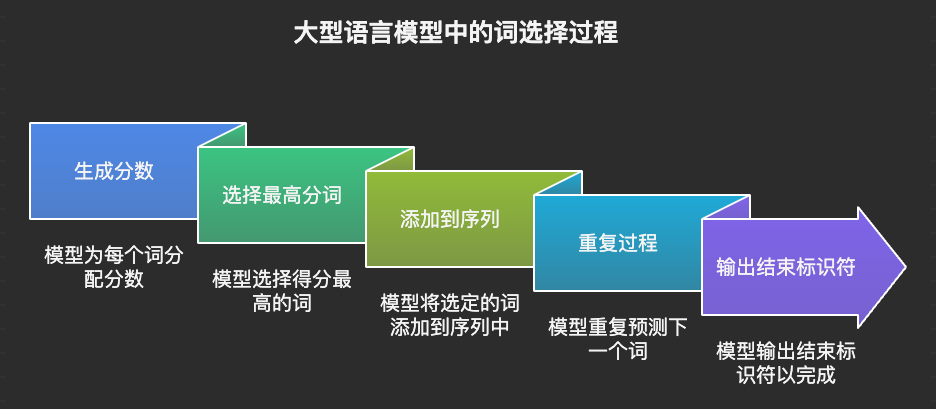
大模型回答的“三步走”流程

要搞懂这两个参数，必须先看大模型是如何预测下一个字的。本质上，Transformer 的核心任务朴素得像猜谜：根据上文，预测下一个最有可能出现的词（Token），重复此过程直到生成结束符。

这个过程可以拆解为三个关键步骤：生成分数 (Logits) –> 转换概率 (Softmax) –>**加权采样 (Sampling)**。

截屏2025-12-04 11.03.52

步骤1: 生成分数（Logits）

我们用一个简单例子说明：当用户提问“帮我推荐一个学习 AI 大模型技术的频道”时，模型会扫描它词表里成千上万个词，并为每一个词打分。这个分数在 AI 领域被称为 Logits。

假设模型打分后，排名前五的词如下：

  • AI：4.2
  • 科技：4.1
  • 奇舞：3.9
  • 自行车：1.8
  • Hello：1.4

打分过程比较复杂，好在跟我们今天的内容关系不大，我们可以暂且忽略。

需要注意的是，在大模型预测下一个词时，会给它所认识的所有词打分，词的总数量大概是在几万到几十万左右。为了方便理解，我们这里只显示分数最高的前五个，其余的全部省略。

在大型语言模型（LLM）完成对所有词汇的评分后，下一步的关键在于如何从这些分数中选择最合适的词作为输出。一种直观且常用的方法是选择得分最高的词。

例如，假设模型在预测序列中的下一个词时，对词汇表中的每个词都进行了评分，比如上面例子中的 “AI” 这个词获得了最高分。那么，模型会选择 “AI” 作为当前步骤的输出。

接下来，模型会将 “AI” 这个词添加到输入序列中，并再次进行下一个词的预测。这意味着模型会重新评估词汇表中的每个词，并为它们分配新的分数。同样，模型会选择得分最高的词作为下一个输出。

这个过程会不断重复，模型逐个输出每一个词，并将每个新生成的词添加到输入序列中，以影响后续词的预测。这种迭代式的生成过程会持续进行，直到模型输出一个特殊的结束标识符（例如 ““）为止。结束标识符的出现标志着文本生成的完成。

截屏2025-12-08 11.10.08

虽然选择得分最高的词是一种简单直接的解码策略，但它也存在一些局限性：

  • 缺乏多样性： 这种策略倾向于选择最常见的词，导致生成的文本缺乏多样性和创造性。模型可能会陷入重复的模式，生成平淡无奇的内容。
  • 对噪声敏感： 如果模型在某个步骤中给出了错误的高分，那么这个错误可能会被放大，导致后续生成的文本偏离预期。
  • 忽略上下文： 虽然模型会将之前生成的词作为输入，但简单地选择最高分可能会忽略更长远的上下文信息，导致生成的文本不连贯或不自然。

这样简单的选择分数最高的词显然是不合适的，我们需要给其他词，比如“科技”或“奇舞”一定机会。聪明的你肯定想到了，把这些词的分数转为概率，让模型按照概率来预测下一个词。提到转换概率，这就轮到大名鼎鼎的 Softmax 函数 登场了。

步骤2: 转换概率（Softmax函数）

Softmax 公式：
$$
\text{Softmax}(z_i) = \frac{e^{z_i/T}}{\sum_{j=1}^{K} e^{z_j/T}}
$$
解析一下这个函数，它这里面的 z_i 代表的就是第 i 个词的分数，K 代表的是词的总数量，而这个输出值就代表第 i 个词的概率了。这里的 T 就是 Temperature，可以先把 T设置为默认值 T = 1，那么这个公式就变为了：
$$
\text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}}
$$
还是以上面的词为例，上面五个词的分数为：z_1（AI） = 4.2、z_2（科技）= 4.1、z_3（奇舞）= 3.9、z_4（自行车）= 1.8、z_5（Hello）= 1.4，那么计算 z_1这个词的概率，上面的公式展开为：
$$
P_1 = \frac{e^{4.2}}{e^{4.2} + e^{4.1}+e^{3.9}+e^{1.8}+e^{1.4}}
$$
截屏2025-12-04 21.36.38

e ≈ 2.718，大致得到的概率如下：

  • AI：36%
  • 科技：32%
  • 奇舞：26%
  • 自行车：3%
  • Hello：2%

Softmax 函数会保证所有词的概率相加为100%。

步骤3：加权采样

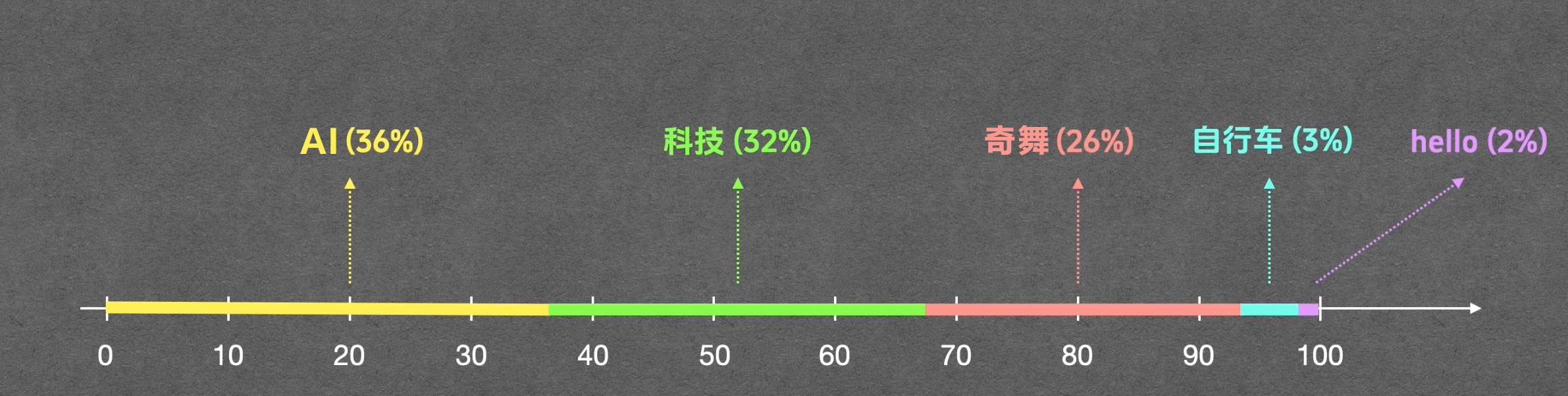
得到了每个词的概率后，就需要根据概率来生成下一个预测的值。一般称这个通过概率来生成预测值的过程为: 加权采样。可以用一个从0到100这个区间的横轴来举例。

”AI“这个词的概率为36%，那么在横轴上给它分配0到36这段区间，科技的概率是32%，我们就给它分配随后的长度为32的这段区间，以此类推。

WechatIMG6955

然后生成一个0到100的随机数。比如说随机数是8，落到了这个[0,36]这个区间，我们就选择 AI。这个就叫做给每个词分配与概率相等的机会。这意味着，虽然“AI”概率最高，但模型也有机会选择“科技”或“奇舞”。这种机制保证了回答的合理性，同时赋予了 AI 创造力和变化。

Temperature 对大模型的作用

截屏2025-12-06 15.13.53

在概率转换模块，我们对 Softmax 函数进行了简化，设置了 T(Temperature) 的取值为1，完整版中，所有的 z 值都会先除以 T，再加入到整体的运算过程中。假如调整 T 的值，会发生什么？

我们对比一下 T=0.1（低温）、T=1.0（标准）、T=2.0（高温）时的概率变化：

词 T=0.1 (低温) T=1.0 (中性) T=2.0 (高温)
AI 71% 36% 30%
科技 26% 32% 28%
奇舞 4% 26% 26%
自行车 0.0% 3% 9%
Hello 0.0% 2% 7%

核心结论：

T < 1 (低温状态)：赢家通吃

  • 原理：当 T 很小时（如 0.1），分数被放大（除以小数等于乘以大数）。指数函数 e^x 会急剧放大差异。高分词的优势被无限拔高，低分词的概率被压缩至近乎为 0。
  • 效果：概率分布变得极度尖锐。模型几乎只选第一名，输出极度稳定、保守。
  • 物理比喻：低温下分子运动缓慢，状态固定（冰）。
  • 适用：代码生成、数学解题（严谨，不容出错）。

T > 1 (高温状态)：众生平等

  • 原理：当 T 很大时（如 2.0），分数被缩小。差异被拉平，指数运算后的结果差别不大。
  • 效果：概率分布变得平缓。高分词优势不再明显，长尾词（如“自行车”）也有了被选中的机会。
  • 物理比喻：高温下分子运动剧烈，状态混乱且不可预测（沸水）。
  • 适用：创意写作、头脑风暴（需要惊喜，容忍偏差）。

通过上面的计算对比，一句话总结 Temperature：它控制的是“贫富差距”。低 T 拉大差距，高 T 缩小差距。

Top P 对大模型的作用

Top P 并不改变概率本身，而是改变选择的范围。Top P 作用在上面的采样环节。在加权采样环节，根据每一个词的概率给它们分配了对等的区间，然后生成了一个随机数，随机数落到哪个区间，就输出哪个区间的值，这样回答就会变得多种多样，但是这也埋下了隐患。

虽然”自行车”只有3%的概率，但只要你试的次数足够多，大模型最后还是很有可能输出”自行车”这三个字的。这肯定不是你想要的答案。大模型的词汇表里面有几十万个词，除了头部的几个合理词，后面基本上都是拖着长长的一串低概率的垃圾词。我们管这些词叫做长尾词。

比如在上面的例子中：”自行车”与 “Hello” 就是长尾词，为了防止模型去选这些长尾词，就需要一个保安, 把这些离谱的选项都拦在门外，这就是 Top P 的作用了。

机制详解：

Top P 的全称为：Top Cumulative Probability（最高累加概率），P指的就是一个概率阈值。模型从高分词开始往下累加概率，一旦累加值超过 P，后面的词全部切掉。

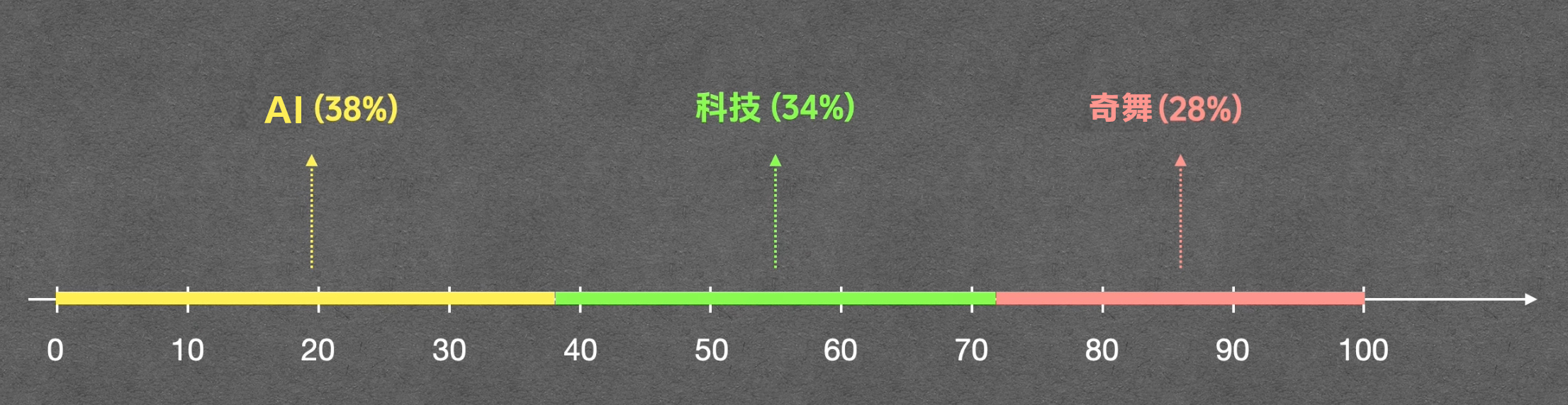
假设我们设置 Top P = 0.9：

  1. AI (36%) -> 累加 36% (<90%，保留)
  2. 科技 (32%) -> 累加 68% (<90%，保留)
  3. 奇舞 (26%) -> 累加 94% (>90%，触发阈值！) -> 保留“奇舞”，截断后续所有词。

结果：“自行车”、“Hello”等长尾词直接被丢弃。剩下的三个词重新归一化概率，然后在它们之间进行采样。

核心结论

Top P 就像一个动态的门槛。

  • **Top P 低 (e.g., 0.1)**：只保留最头部的几个词，极度保守。
  • **Top P 高 (e.g., 0.9)**：允许更多可能性的词进入候选池，保留多样性，同时切除极不靠谱的尾部。

所以总结一下：

参数 低值效果 高值效果 适用场景 与另一参数区别
Temperature 差距放大，赢家通吃，稳定 差距缩小，均等，多样 低：代码/数学；高：小说/idea 全局概率分布
Top P 头部窄，切长尾，保守 门槛宽，兼容，随机 低：专业Q&A；高：开放讨论 尾部过滤阈值

建议

  1. 通常只调整其中一个：虽然可以同时调整，但为了控制变量，主流建议是固定一个（如 Top P = 1），只调另一个。
  2. 发散思维场景（写小说、想点子）：
    • 推荐：设置 0.8 <= T <= 1.2 左右 或 设置 Top P 为 0.9左右。
    • 让模型“发散”一会儿，但别太离谱。
  3. 严谨逻辑场景（写代码、提取数据）：
    • 推荐：设置 0.0 <= T <= 0.2 或 0.1 <= Top P <= 0.2 左右。
    • 确保模型只选概率最高的那个词，保证逻辑的连贯和语法的正确。

理解了这两个参数，你就不是在盲目地“炼丹”，而是在精准地调试你的数字引擎。